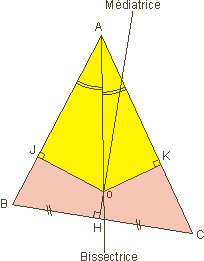
Soit un triangle quelconque
ABC dont nous traçons la bissectrice en A et la médiatrice
de [BC] en H.
Comme le triangle est quelconque, la médiatrice et la bissectrice
ne sont pas confondues et se coupent en O.
Traçons les perpendiculaires aux cotés [AB] et [AC], passant
par O, ce qui nous donne respectivement les points J et K.
Première
constatation :
Les deux triangles AOJ et AOK sont égaux, puisqu'ils ont des angles égaux et une hypothénuse commune.
Deuxième constatation :
Les distances OB et
OC sont égales puisque le point O est sur le médiatrice.
Notons R = OB = OC
En traçant ci-contre les deux triangles égaux AOJ et AOK, et en traçant le même segment de longueur R, on obtient deux figures totalement symétriques.
D'où AB = AC

Nous venons de démontrer
qu'un triangle quelconque est isocèle.
En reprenant la même démonstration, avec une bissectrice
en B, on montrerait de la même manière que BA = BC.
CONCLUSION :
UN
TRIANGLE QUELCONQUE EST ÉQUILATÉRAL !
Cette nouvelle
propriété simplifie largement la plupart des problèmes
de géométrie.
L'auteur décline toute responsabilité concernant l'utilisation qui serait faite de cette conclusion.
Pour les sceptiques, s'il en reste :
La question
qui est souvent posée est :
"oui, mais si la bissectrice et la médatrice se coupent à
l'extérieur du triangle ?"
Réponse
: bein, pas de problème...
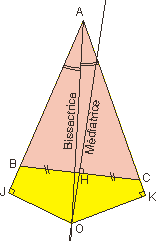
Regardez la
figure ci-contre. Le point O est à l'extérieur du triangle
ABC.
Les triangles AOJ et AOK sont toujours égaux, les distances OB
et OC aussi.
Il faut maintenant tracer les segments de longueur R à l'intérieur
des triangles AOJ et AOK, c'est tout...
Et la démonstration reste valable !